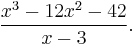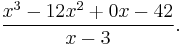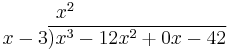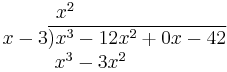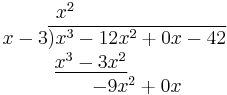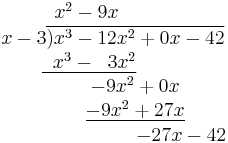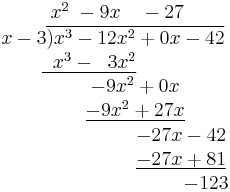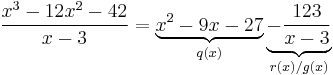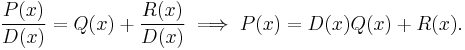Polynomial long division

In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division. It can be done easily by hand, because it separates an otherwise complex division problem into smaller ones.

1 Example
2 Division transformation
3 Applications
- 3.1 Factoring polynomials
- 3.2 Finding tangents to polynomials
4 See also
5 Notes

Example

Find

$\frac{x^3 - 12x^2 - 42}{x-3}.$

The problem is written like this:

$\frac{x^3 - 12x^2 %2B 0x - 42}{x-3}.$

The quotient and remainder can then be determined as follows:

Divide the first term of the numerator by the highest term of the denominator (meaning the one with the highest power of x, which in this case is x). Place the result above the bar (x³ ÷ x = x²).

$\begin{matrix} x^2\\ \qquad\qquad\quad x-3\overline{) x^3 - 12x^2 %2B 0x - 42} \end{matrix}$
Multiply the denominator by the result just obtained (the first term of the eventual quotient). Write the result under the first two terms of the numerator (x² · (x − 3) = x³ − 3x²).

$\begin{matrix} x^2\\ \qquad\qquad\quad x-3\overline{) x^3 - 12x^2 %2B 0x - 42}\\ \qquad\;\; x^3 - 3x^2 \end{matrix}$
Subtract the product just obtained from the appropriate terms of the original numerator (being careful that subtracting something having a minus sign is equivalent to adding something having a plus sign), and write the result underneath ((x³ − 12x²) − (x³ − 3x²) = −12x² + 3x² = −9x²) Then, "bring down" the next term from the numerator.

$\begin{matrix} x^2\\ \qquad\qquad\quad x-3\overline{) x^3 - 12x^2 %2B 0x - 42}\\ \qquad\;\; \underline{x^3 - 3x^2}\\ \qquad\qquad\qquad\quad\; -9x^2 %2B 0x \end{matrix}$
Repeat the previous three steps, except this time use the two terms that have just been written as the numerator.

$\begin{matrix} \; x^2 - 9x\\ \qquad\quad x-3\overline{) x^3 - 12x^2 %2B 0x - 42}\\ \;\; \underline{\;\;x^3 - \;\;3x^2}\\ \qquad\qquad\quad\; -9x^2 %2B 0x\\ \qquad\qquad\quad\; \underline{-9x^2 %2B 27x}\\ \qquad\qquad\qquad\qquad\qquad -27x - 42 \end{matrix}$
Repeat step 4. This time, there is nothing to "pull down".

$\begin{matrix} \qquad\quad\;\, x^2 \; - 9x \quad - 27\\ \qquad\quad x-3\overline{) x^3 - 12x^2 %2B 0x - 42}\\ \;\; \underline{\;\;x^3 - \;\;3x^2}\\ \qquad\qquad\quad\; -9x^2 %2B 0x\\ \qquad\qquad\quad\; \underline{-9x^2 %2B 27x}\\ \qquad\qquad\qquad\qquad\qquad -27x - 42\\ \qquad\qquad\qquad\qquad\qquad \underline{-27x %2B 81}\\ \qquad\qquad\qquad\qquad\qquad\qquad\;\; -123 \end{matrix}$

The polynomial above the bar is the quotient, and the number left over (−123) is the remainder.

$\frac{x^3 - 12x^2 - 42}{x-3} = \underbrace{x^2 - 9x - 27}_{q(x)} \underbrace{-\frac{123}{x-3}}_{r(x)/g(x)}$

The long division algorithm for arithmetic can be viewed as a special case of the above algorithm, in which the variable x is replaced by the specific number 10.

Division transformation

Polynomial division allows for a polynomial to be written in a divisor–quotient form which is often advantageous. Consider polynomials P(x), D(x) where degree(D) < degree(P). Then, for some quotient polynomial Q(x) and remainder polynomial R(x) with degree(R) < degree(D),

$\frac{P(x)}{D(x)} = Q(x) %2B \frac{R(x)}{D(x)} \implies P(x) = D(x)Q(x) %2B R(x).$

This rearrangement is known as the division transformation, and derives from the arithmetical identity 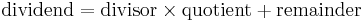${\mathrm{dividend} = \mathrm{divisor} \times \mathrm{quotient} %2B \mathrm{remainder} }$ .^[1]

Applications

Factoring polynomials

Sometimes one or more roots of a polynomial are known, perhaps having been found using the rational root theorem. If one root r of a polynomial P(x) of degree n is known then polynomial long division can be used to factor P(x) into the form (x - r)(Q(x)) where Q(x) is a polynomial of degree n–1. Q(x) is simply the quotient obtained from the division process; since r is known to be a root of P(x), it is known that the remainder must be zero.

Likewise, if more than one root is known, a linear factor (x – r) in one of them (r) can be divided out to obtain Q(x), and then a linear term in another root, s, can be divided out of Q(x), etc. Alternatively, they can all be divided out at once: for example the linear factors x– r and x – s can be multiplied together to obtain the quadratic factor x² – (r + s)x + rs, which can then be divided into the original polynomial Q(x) to obtain a quotient of degree n – 2.

In this way, sometimes all the roots of a polynomial of degree greater than four can be obtained, even though that is not always possible. For example, if the rational root theorem can be used to obtain a single (rational) root of a quintic polynomial, it can be factored out to obtain a quartic (fourth degree) quotient; the explicit formula for the roots of a quartic polynomial can then be used to find the other four roots of the quintic.

Finding tangents to polynomials

Polynomial long division can be used to find the equation of the line that is tangent to a polynomial at a particular point.^[2] If R(x) is the remainder when P(x) is divided by (x – r )² — that is, by x² – 2rx + r ² — then the equation of the tangent line to P(x) at x = r is y = R(x) (regardless of whether or not r is a root of the polynomial).

Notes

^ S. Barnard (2008). Higher Algebra. READ BOOKS. p. 24. ISBN 1443730866.
^ Strickland-Constable, Charles, "A simple method for finding tangents to polynomial graphs", Mathematical Gazette 89, November 2005: 466-467.